Profiling Serial Merge Sort

本文最后更新于 2023年12月14日 下午

MIT 6.172 Performance Engineering of Software Systems “Homework 2: Profiling Serial
Merge Sort”

文档地址:https://ocw.mit.edu/courses/6-172-performance-engineering-of-software-systems-
fall-2018/796439e646c02f44348d50b1836ff7f9_MIT6_172F18hw2.pdf

代码地址:https://ocw.mit.edu/courses/6-172-performance-engineering-of-software-systems-
fall-2018/b050ca87021170ea0319bce601ae17d3_MIT6_172F18_hw2.zip

本次实验使用的Clang版本为clang 16.0.6

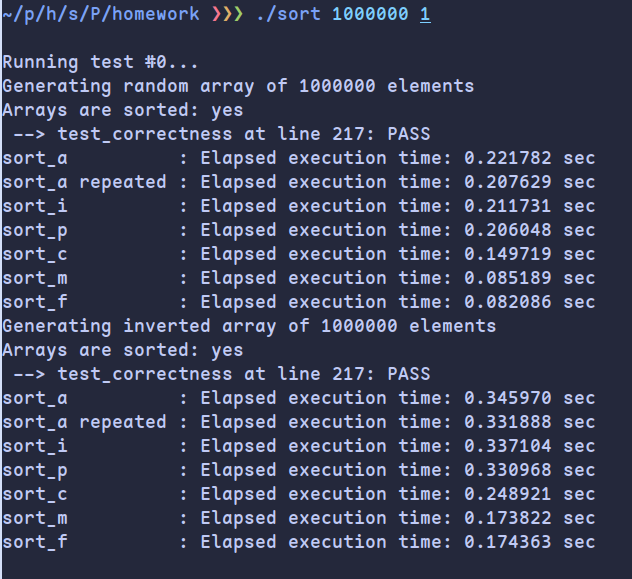
Checkoff Item 1

branch misses, clock cycles and instructions如下

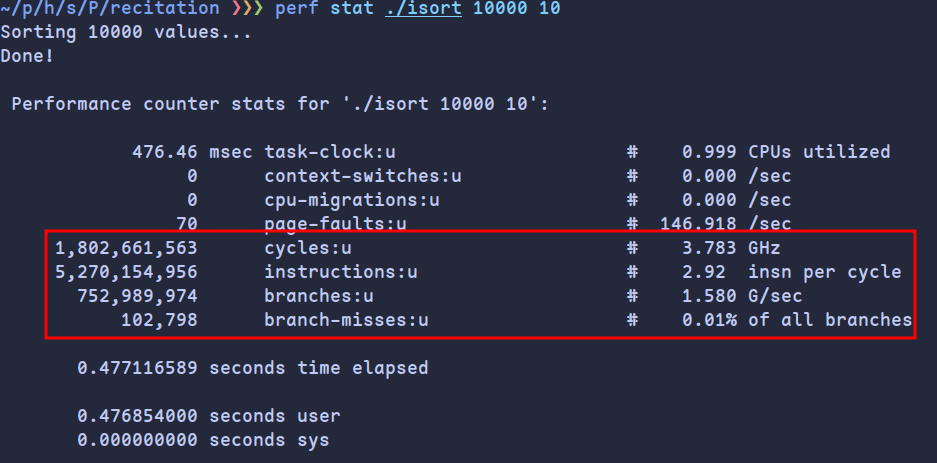
image-20231210171240889

进入perf report后选择Annotate isort可以查看每条汇编指令对性能的占用，可以发现主要的bottleneck在while(index >= left && *index > val)中：

image-20231210005020473

Checkoff Item 2

lscpu结果如下：

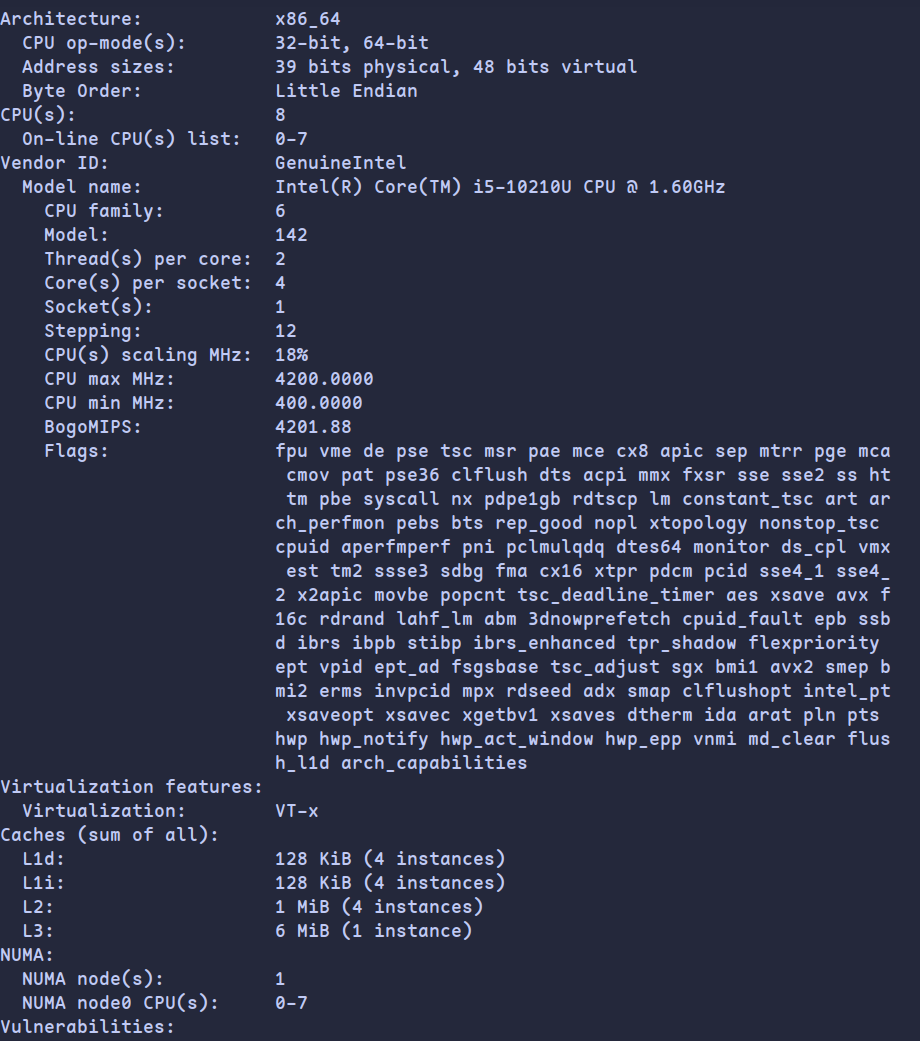
image-20231210011247692

可以看到cpu缓存为：

Caches (sum of all):
  L1d:                   128 KiB (4 instances)
  L1i:                   128 KiB (4 instances)
  L2:                    1 MiB (4 instances)
  L3:                    6 MiB (1 instance)

D1 and LLd misses

要查看D1 and LLd misses，需要添加--cache-sim=yes选项

运行valgrind --tool=cachegrind --cache-sim=yes ./sum

得到结果为：

==81043== D refs:          610,045,970  (400,033,960 rd   + 210,012,010 wr)
==81043== D1  misses:      100,545,938  ( 99,920,504 rd   +     625,434 wr)
==81043== LLd misses:       84,952,267  ( 84,326,856 rd   +     625,411 wr)
==81043== D1  miss rate:          16.5% (       25.0%     +         0.3%  )
==81043== LLd miss rate:          13.9% (       21.1%     +         0.3%  )

从结果可以看出，缓存等级越高（L3），缓存命中率越大。因为高等级的缓存的大小更大，lscpu的信息也验证这一点

另外，读操作的缓存不命中率比写操作更多，从代码可以看出原因：

写操作：

for (i = 0; i < U; i++) {
  data[i] = i;
}

读操作：

for (i = 0; i < N; i++) {
  int l = rand_r(&seed) % U;
  val = (val + data[l]);
}

写操作是顺序写，具有良好的空间局部性，缓存命中率更高，读操作是随机读，缓存命中率低

所以结果符合预期

Bring down the number of cache misses

L3缓存是6MB，数组中元素是32位，所以理论上将U改为6x1024x1024x8/32=1572864即可让数据全部缓存在L3中从而将不命中率降为0

验证结果：

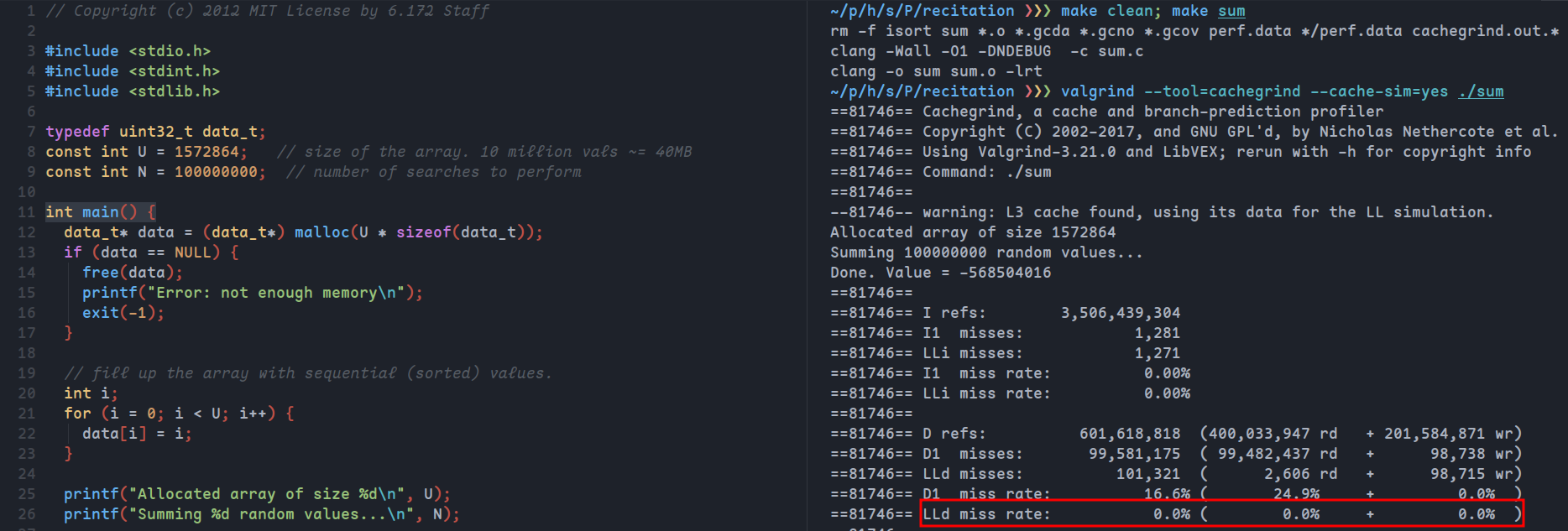
image-20231210015847087

如图所示，LLd的缓存不命中率几乎为0

同样若想让L1的不命中率为0，由于L1d为128kb，并且有4个实例，所以应该修改数据为32kb，即修改U为8192：

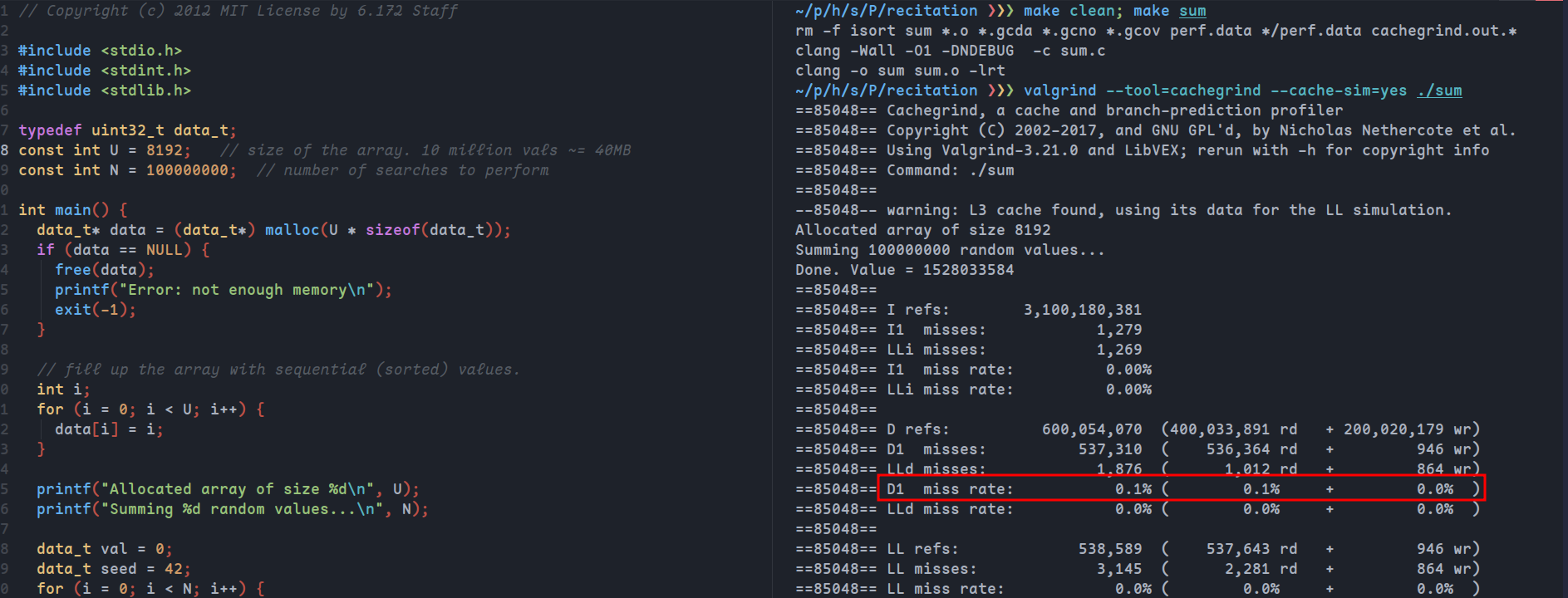
image-20231210020601649

可以看到D1的缓存不命中率几乎为0

而对于变量N:

在缓存无法放满数据的情况下，由于随机性，随机读有概率导致不命中，而更小的N值将减少随机读操作带来的不命中率

Write-Up 1

结果对比

由于Clang版本的问题，-always-inline选项已被移出，从官方文档中找到替代选项：

-finline-hint-functions

Inline functions which are (explicitly or implicitly) marked inline

替换后运行命令：

make DEBUG=1
valgrind --tool=cachegrind --cache-sim=yes --branch-sim=yes ./sort 100000 1 > result_o0 2>&1
make DEBUG=0
valgrind --tool=cachegrind --cache-sim=yes --branch-sim=yes ./sort 100000 1 > result_o3 2>&1
git difftool result_o0 result_o3 --no-index

得到结果（左：DEBUG=1，右：DEBUG=0）

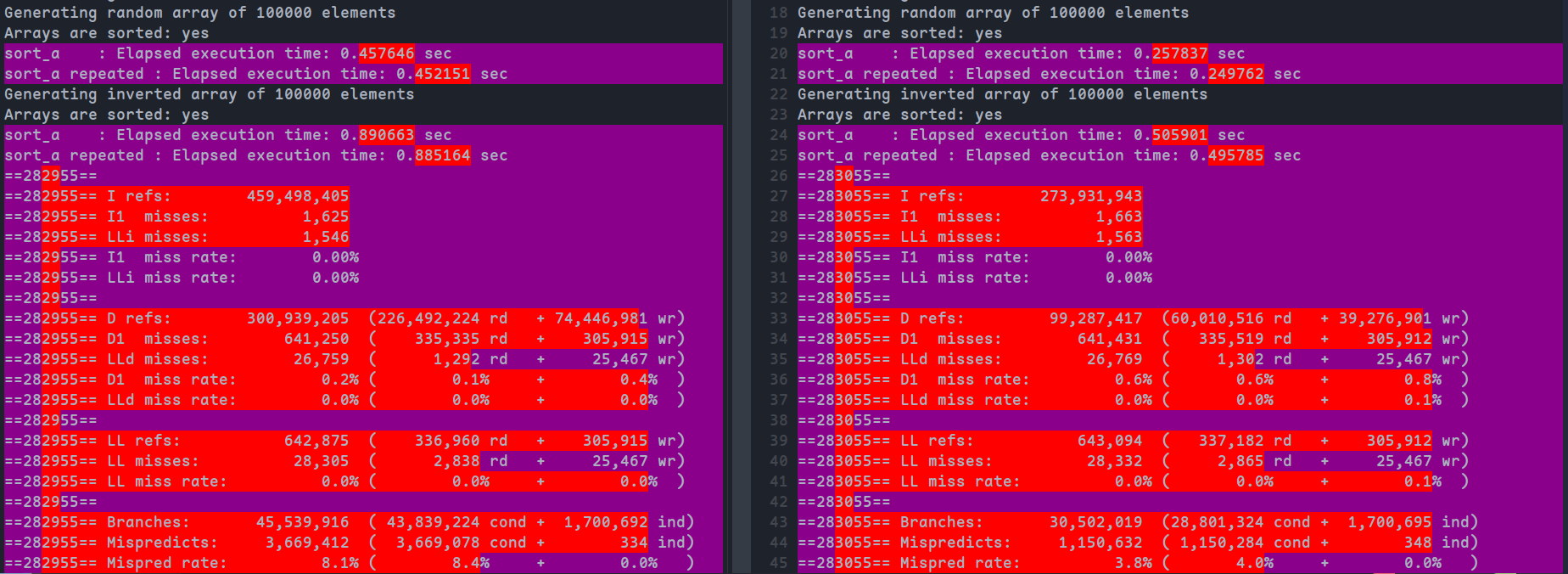
image-20231210182628050

可以看到

时间上，DEBUG=0的情况下运行时间减少了约一半

指令数上，DEBUG=0的情况下总共的指令数同样减小约一半，但是由于总指令数减小，而两者的缓存不命中率次数差不多，所以缓存不命中比率上升，比DEBUG=1大概提升两倍；而对于分支预测，DEBUG=0会带来更好的分支预测命中数，同时分支的情况也有所减小

使用指令数替换时间作为评估指标的优缺点

优点：

  • 计量指令数比测量时间更简单
  • 如果以时间为评估，多次测量的结果会受外部因素的影响，存在误差，而以指令数为评估，多次测量结果一样，更为直观
  • 可以直观衡量缓存命中/未命中、分支预测等优化因素的变化情况

缺点：

  • 指令数为指标不考虑单个指令的复杂性，某些指令可能需要更长的时间来执行，从而导致即使指令数较低，执行速度也会变慢
  • 指令数为指标无法衡量缓存命中/未命中、分支预测等优化因素带来的时间收益
  • 指令数为指标不考虑外部因素，例如 I/O 操作、网络延迟等因素可能会显著影响程序的整体性能，所以仅依靠指令数可能无法准确表示实际性能

两个指标各有优缺点，而同时以指令数和时间作为评估指标可以更全面的衡量程序性能

Write-up 2

查看是否有内联：

将sort_a.c的代码复制到sort_i.c中，并将函数名全部改为<function>_i，在main.c中添加sort_i的测试代码

关于内联的控制，由于新版Clang -always-inline选项已经弃除，可以添加__attribute__((always_inline))属性强制内联，另外为防止编译器自动内联，以DEBUG=1模式编译并运行

以函数copy_i为例，首先查看原始代码的汇编生成clang -O0 -S sort_i.c -o sort_i.s

搜索copy_i关键字可以发现调用过程：

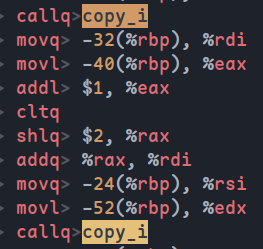
image-20231211005329750

然后在函数前添加__attribute__((always_inline))属性，再次生成汇编代码，并不能找到调用copy_i的语句，说明内联成功

此外在perf report中也无法在对应位置找到与函数跳转部分，说明内联成功

是否内联对比：

为函数merge_i，copy_i，memory_free，memory_alloc添加内联，为使结果差异更明显，修改运行参数为1000000，编译并运行命令：valgrind --tool=cachegrind --cache-sim=yes --branch-sim=yes ./sort_inline_o0 1000000 1 > result_inline_o0 2>&1

得到比较结果如下（左：内联，右：未内联）：

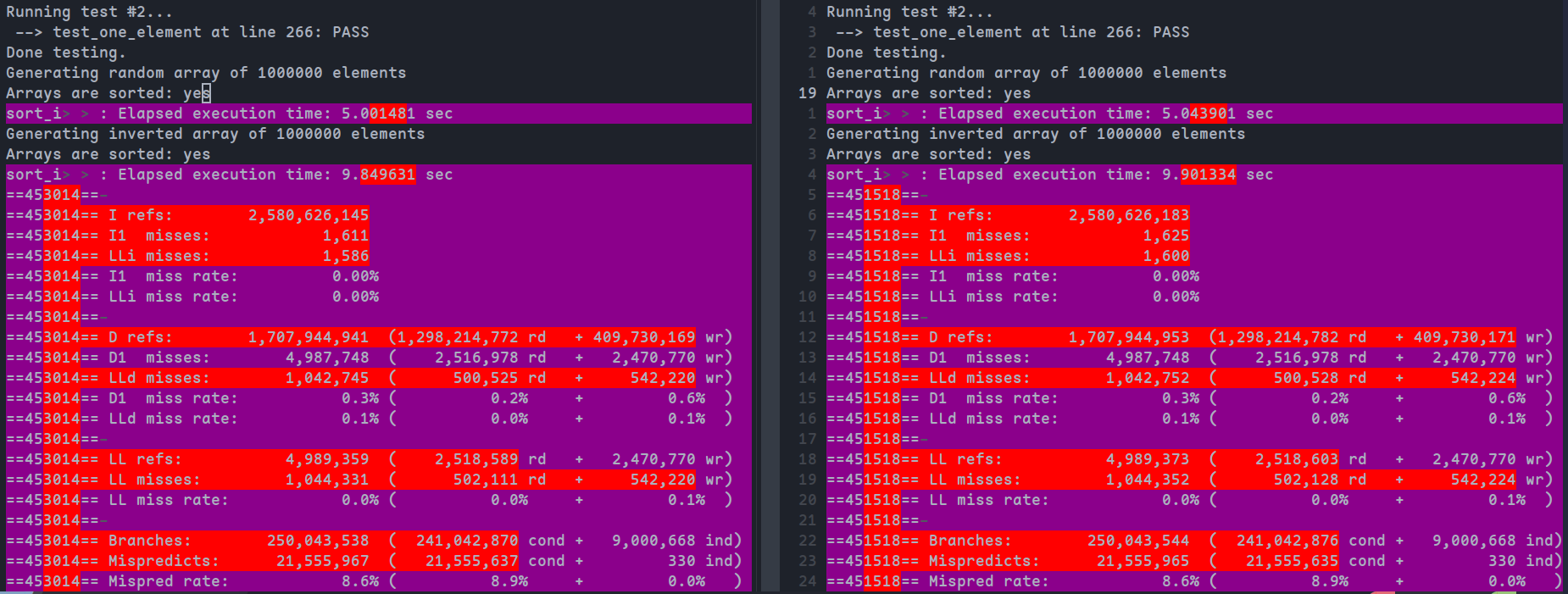
image-20231211010835554

可以看到，尽管没有显著差距，但是内联后的运行时间，指令数，缓存未命中率均有少量下降，而分支误预测数增加了两个，可以忽略

Write-up 3

为sort_i添加inline，与未内联结果对比如下：

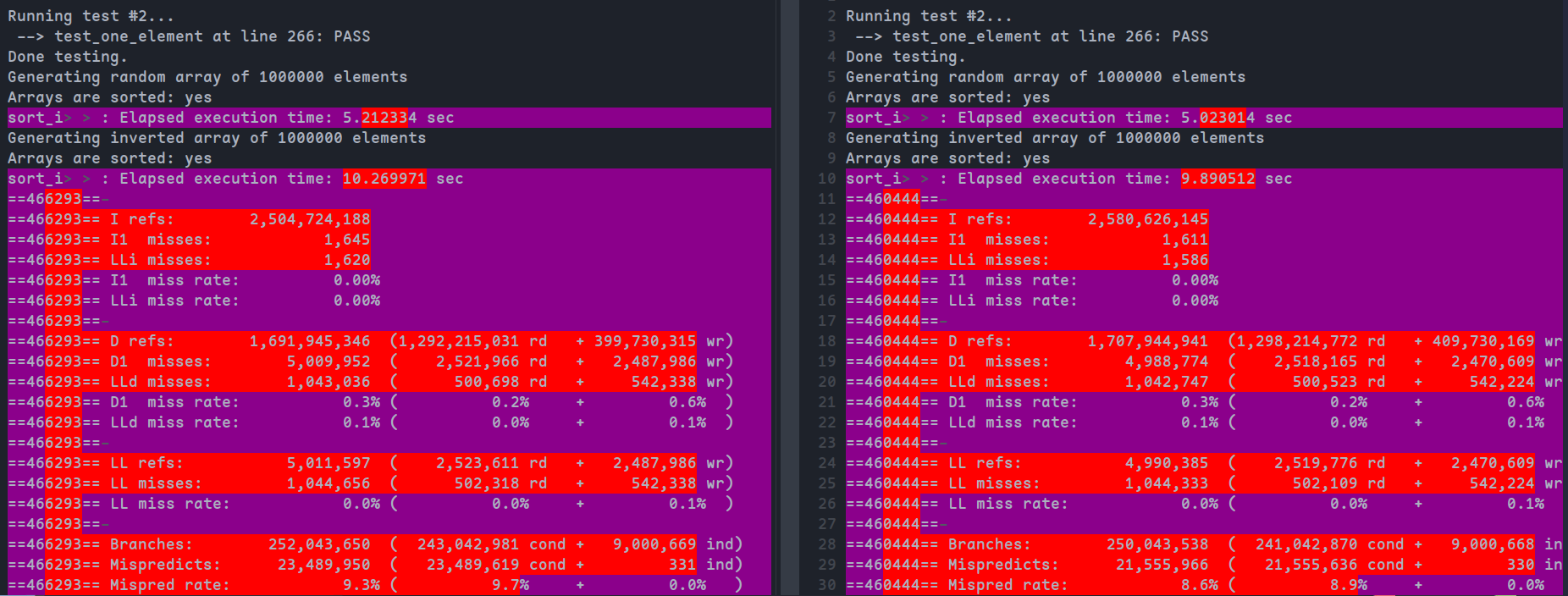
image-20231211013646145

可以看到性能有所折损，缓存未命中率和分支误预测数均有上升

展开递归函数可能会导致代码膨胀，通过这些指标我们可以认为：

  • 递归函数的展开导致代码体积变大，不能放入缓存的部分变多，从而导致I1 misses和LLi misses的增大
  • 展开会导致重复的分支，从而增大分支数
  • 会增加更多的变量来维护数据，从而增大数据缓存未命中

Write-up 4

复制代码后，将所有以下标形式访问数组的语句array[x]修改为以指针形式访问*(array+x)

在DEBUG=1模式下分别编译并运行

运行命令如下：

valgrind --tool=cachegrind --cache-sim=yes --branch-sim=yes ./sort_array_o0 1000000 1 > result_array_o0 2>&1
valgrind --tool=cachegrind --cache-sim=yes --branch-sim=yes ./sort_points_o0 1000000 1 > result_points_o0 2>&1

对比结果：

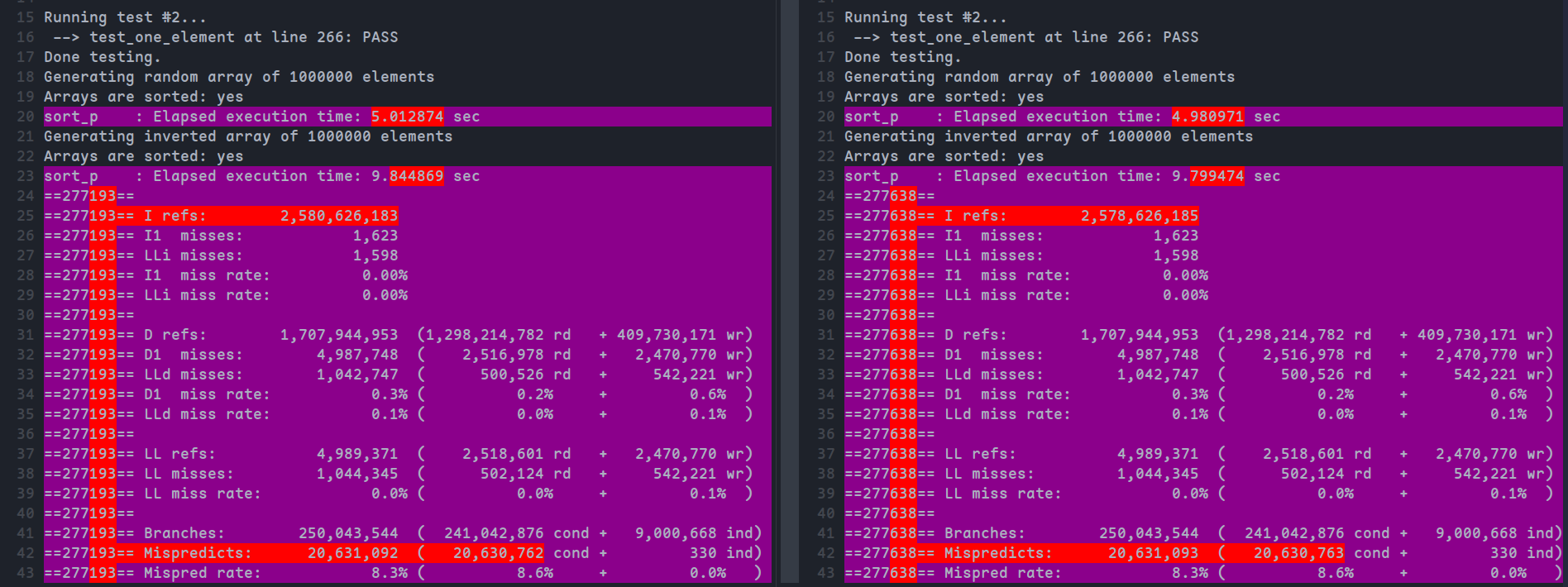
image-20231210181346742

从结果上看，指针形式的运行速度略微更快（5.012874->4.980971），总操作数有所下降（2,580,626,183->2,578,626,185），分支预测未命中次数多了一个，可以忽略，其他指标无明显变化

对于为什么指针形式可以提高性能，解释如下：

实际上在时间上两者的差距并不明显，通过命令clang -O0 -S -o p_point.s sort_p.c生成两个版本的汇编代码（左：数组，右：指针）：

image-20231210195215140

可以发现唯一的区别在与第二次调用copy_p函数处（copy_p(&*(A + q + 1), right, n2);）

%rdi是函数第一个参数，可以发现数组两者对参数的处理顺序不一样，数组版本是先将偏移量计算好，然后得到地址，而指针版本是直接计算两次地址，整体上比数组下标版本少一个指令

为什么这样可以提升性能呢，主要可以观察到多出的命令是cltq，用于扩展eax寄存器到64位。由于在64位cpu上，地址是64位，而变量q是32位，如果先计算q+1，为减少计算量所以是根据32位来计算，但最后和指针计算仍然要扩展到64位，而如果先和指针计算，则一开始就按照64位计算。在这个例子中，扩展32位到64位的性能损耗大于32位加法对64位加法的性能提升，所以整体上性能是有折损的，因此指针形式可以提高性能（仅针对这一例子，实际情况要根据具体的指令来看）

Write-up 5

和之前一样，复制代码并替换函数名并在main中添加测试

此题要求我们使用另外的排序算法替换递归的基本情况，这里则使用其提供的插入排序算法

修改代码如下:

#define BASE 10
void isort(data_t *begin, data_t *end);

// A basic merge sort routine that sorts the subarray A[p..r]
void sort_c(data_t *A, int p, int r) {
  assert(A);
  if ((p + BASE) < r) {
    int q = (p + r) / 2;
    sort_c(A, p, q);
    sort_c(A, q + 1, r);
    merge_c(A, p, q, r);
  } else {
    isort(&A[p], &A[r]);
  }
}

添加BASE条件，如果元素小于BASE个，则使用插入排序

由于插入排序最好的时间复杂度为O(n)，其在小规模的数据集下可能会有更好的表现，替换BASE CASE可以获得性能提升，BASE=10，N=1000000时对比结果如下（左：coarsening，右：未coarsening）：

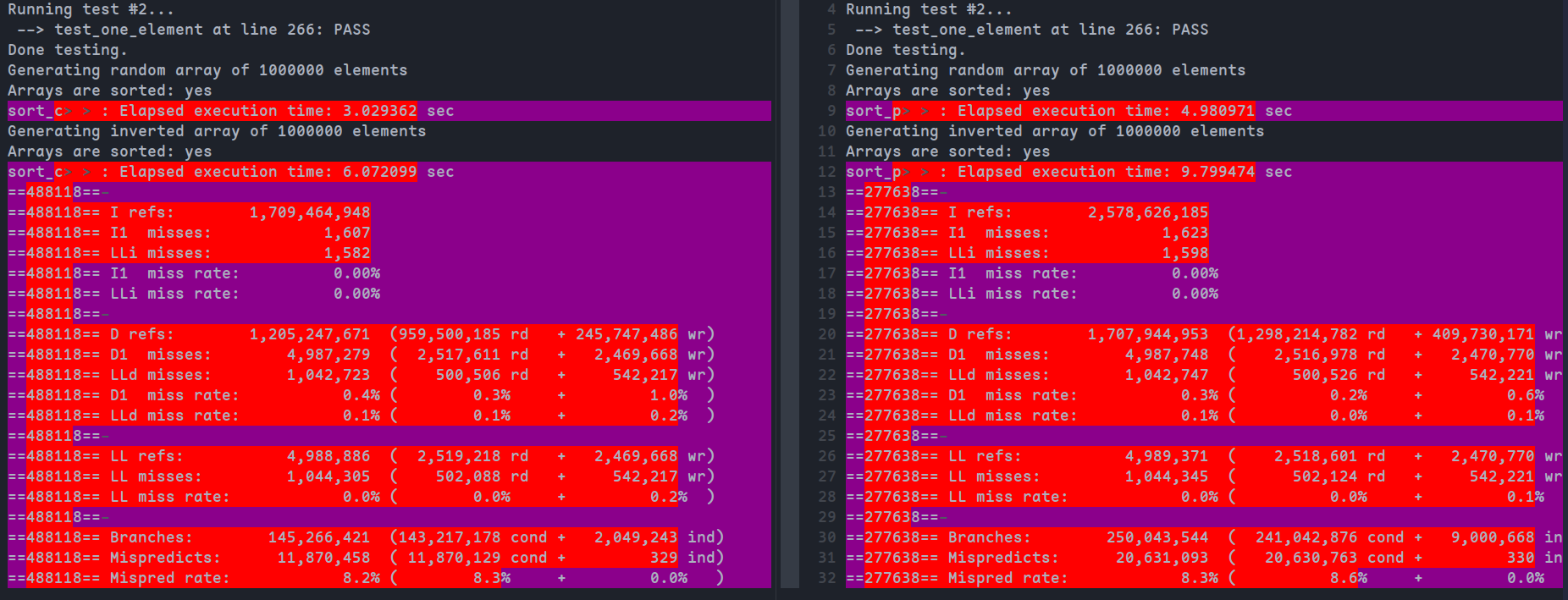
image-20231211022633606

可以看到时间快了1-3s，数据引用有所减小，但在缓存命中上并没有明显差距，而分支总数减少了近一半，因为插入排序规避了一部分归并排序的分支判断

chose the number of elements

首先较小的BASE对缓存友好，其次插入排序的最坏时间复杂度为n2n^2，最好复杂度为O（n），另一方面替换BASE CASE为插入排序可以提升性能，减少分支判断（利用较好的情况），所以我们需要进行折中，选择合适的BASE

以运行时间为指标，N=10000000，DEBUG=1，选择不同的BASE值，得到变化曲线如下

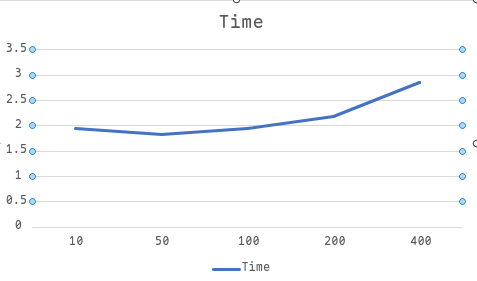
image-20231211233601991

我们在BASE=50处得到较好的效果，而之后提升BASE值都会增加运行时间

Write-up 6

修改代码如下：

  ...

  mem_alloc(&left, n1 + 1);
  // mem_allom(&right, n2 + 1);
  if (left == NULL) {
    mem_free(&left);
    // mem_free(&right);
    return;
  }

  copy_m(&*(A + p), left, n1);
  *(left + n1) = UINT_MAX;
  // *(right + n2) = UINT_MAX;

  int i = 0;
  int j = 0;

  for (int k = p; k <= r; k++) {
    if (*(left + i) <= *(A + n1 + j) || j >= n2) {
      *(A + k) = *(left + i);
      i++;
    } else {
      *(A + k) = *(A + n1 + j);
      j++;
    }
  }
  mem_free(&left);
  // mem_free(&right);
}

将原先为右半边数组额外分配的数组去除，直接利用原数组，从而减少内存分配的开销

修改前后结果对比如下（更换diff工具，左：修改后，右：修改前）：

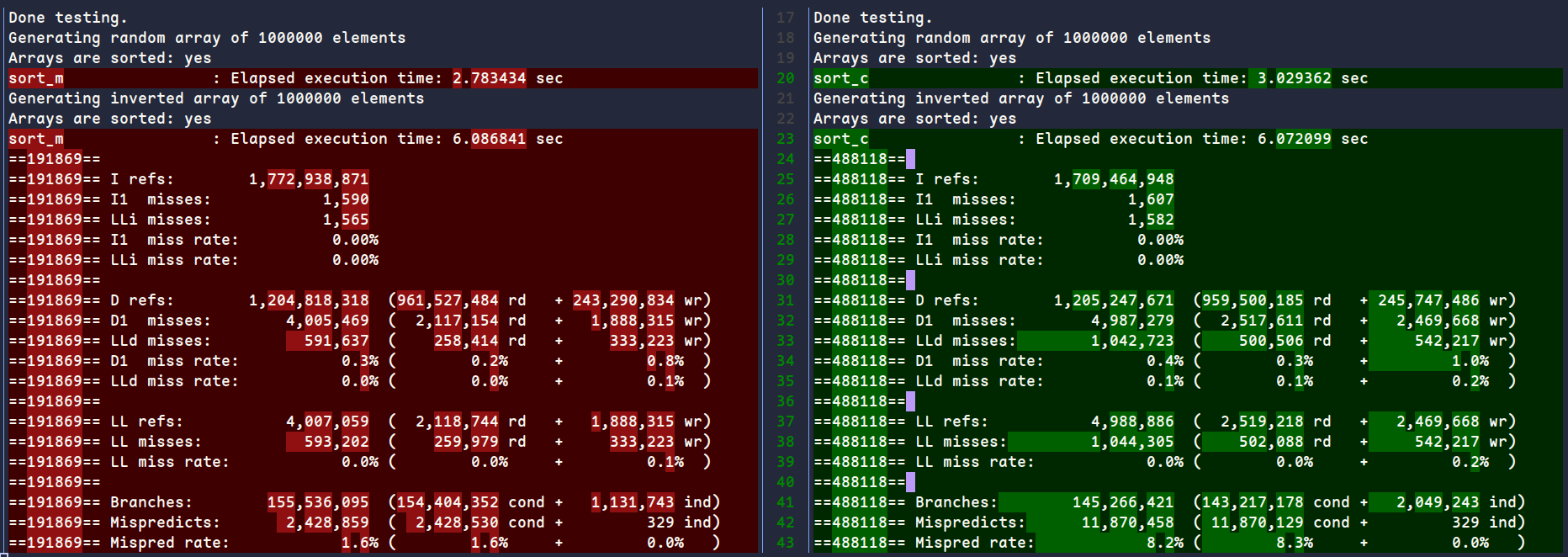
image-20231212004840483

可以看到运行时间有一定减少，因为添加了j >= n2的条件判断，分支数上有一定增加，因为没有额外的内存分配，数据引用数和缓存未命中数也有显著减少

Can a compiler automatically make this optimization

此部分优化和算法逻辑有一定关系，编译器无法直接判断是否是没必要的内存分配，如果直接进行优化会有潜在的内存覆盖风险

用clang以O3查看汇编代码可以发现仍然分配了两段内存：

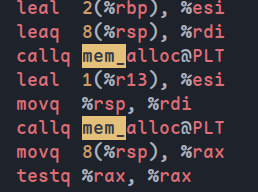
image-20231212003254734

Write-up 7

修改代码如下：

void sort_f(data_t *A, int p, int r) {
...
  data_t *left = 0;
  int q = (p + r) / 2;
  int n1 = q - p + 1;
  mem_alloc(&left, n1 + 1);
  if (left == NULL) {
    mem_free(&left);
    return;
  }
  sort_with_left(A, p, r, left);
  mem_free(&left);
...
void sort_with_left(data_t *A, int p, int r, data_t *left) {
  assert(A);
  if ((p + BASE) < r) {
    int q = (p + r) / 2;
    sort_with_left(A, p, q, left);
    sort_with_left(A, q + 1, r, left);
    merge_f(A, p, q, r, left);
  } else {
    isort(&A[p], &A[r]);
  }
}

直接在sort函数中添加内存分配步骤，然后实现额外的递归函数传递left，从而不用在每次递归时重新分配内存

修改前后对比如下（左：修改后，右：修改前）

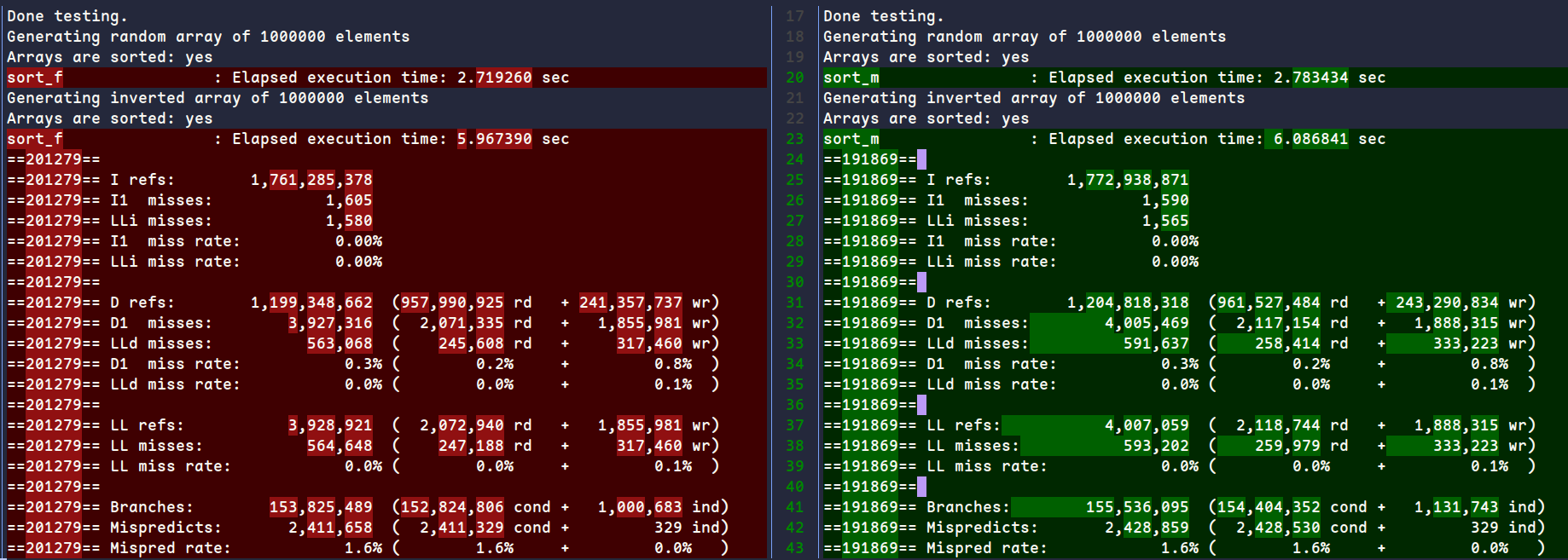
image-20231212010959772

可以看到时间、指令数、数据引用、缓存未命中率、分支数和分支误预测率均有所下降

explain the differences

这一步实际是对mem_alloc和mem_free的调用次数的优化

对比perf report结果可以发现未优化时mem_alloc和mem_free的时间占据更多，而优化后的时间占据几乎没有：

image-20231212014320719

最终结果

所有修改代码已放在homework文件夹下

最终结果如下，可以看到每步修改对程序性能的优化：

image-20231212012743599

实验报告 > 软件系统优化
#perf #性能优化
Profiling Serial Merge Sort
https://gentlecold.top/20231214/profiling-serial-merge-sort/
作者
GentleCold
发布于
2023年12月14日
许可协议