CMU10414-Fall2022课程笔记

课程笔记

softmax

• 监督学习/无监督学习
• 假设函数/损失函数/优化方法
• 有些err函数是不可微分的，所以用softmax(激活函数，引入非线性层)->交叉熵(-log)作为损失函数
• 转换为优化问题，使用梯度下降/随机梯度下降

设$m$为样本数，$n$为特征数，$k$为分类数

$h(x)$为假设函数，$h_y(x)$为在$label=y$上的分量

softmax为：

$$z_i = e^{h_i(x)}/ \sum_{k=1}^n e^{h_k(x)} \\$$

softmax存在数值爆炸问题，可以对$h_k(x)-max(h(x))$，映射范围为0~1，每个分量和为1

softmax_loss为：

$$\begin{align*} l(h, y) &= -log(e^{h_y(x)} / \sum_{k=1}^n e^{h_k(x)}) \\ &= -h_y(x) + log(\sum_{k=1}^n e^{h_k(x)}) \end{align*}$$

对$h_i(x)$求偏导：

$$\frac{\partial l(h,y)}{\partial h_i}=-1\{i=y\}+z_i$$

如果$h(x)=\Theta^T \cdot x$，$\Theta \in R^{n\times k}$，则偏导为：

$$\frac{\partial l(h,y)}{\partial \theta_{i,j}} =(-1\{i=y\}+z_i)\cdot x_{i,j}$$

批量梯度下降，选择$B$个样本然后算出梯度平均，然后对参数立即更新

neural networks

• 引入非线性层
• 有几个W（权重）就是几层网络

• 对于一个两层网络的梯度推导：

• 对于多层：

通过$G_{L+1}$反向传播计算到$G_i$，从而可以算出梯度（需要保留前向传播算出的$Z_i$）

automatic differentiation

• forward mode AD

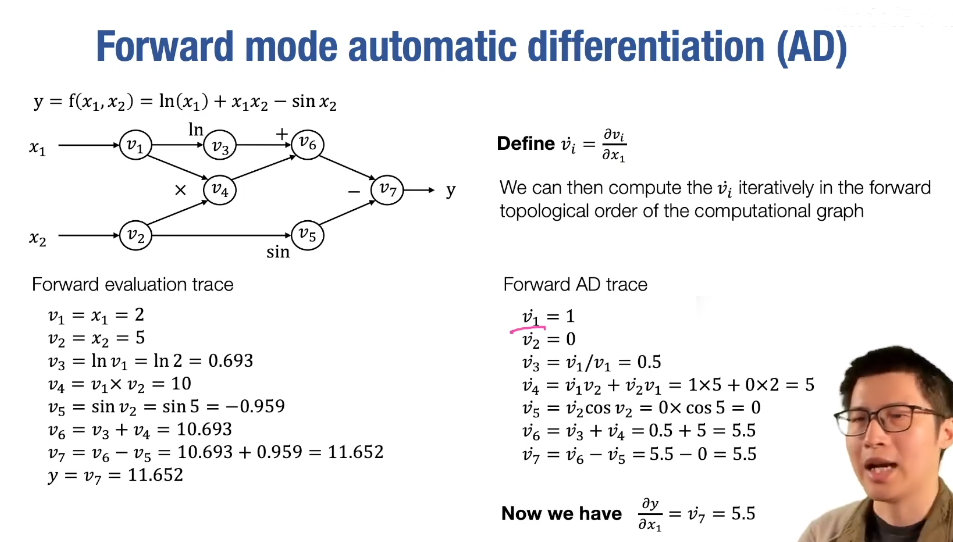
这种方法一次只能计算出$\frac{\partial v_7}{\partial x_1}$，对于$\frac{\partial v_7}{\partial x_2}$还要再传播一次

• reserve mode AD

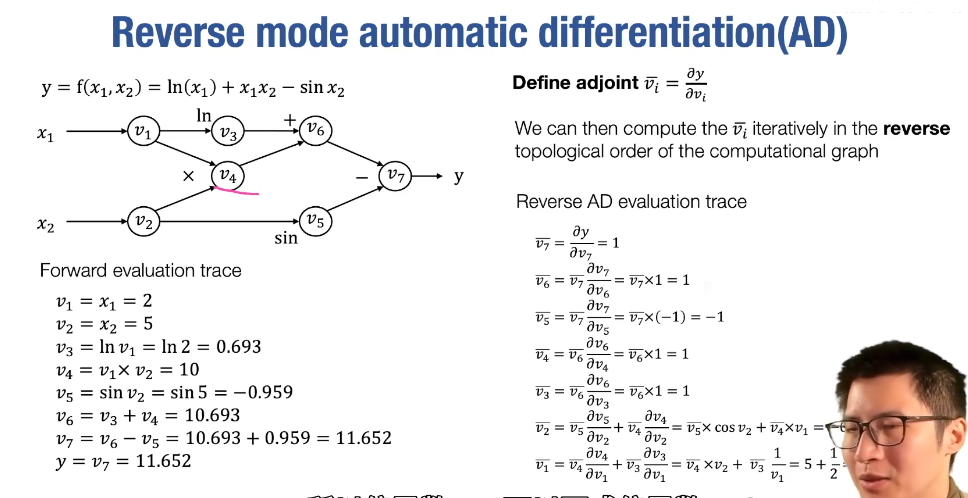
使用反向的方法可以一次推导出所需要的所有偏导数

• reserve mode AD by extending computational graph

$$\overline{v_{i->j}}=\overline{v_i}\frac{\partial v_i}{\partial v_j}$$

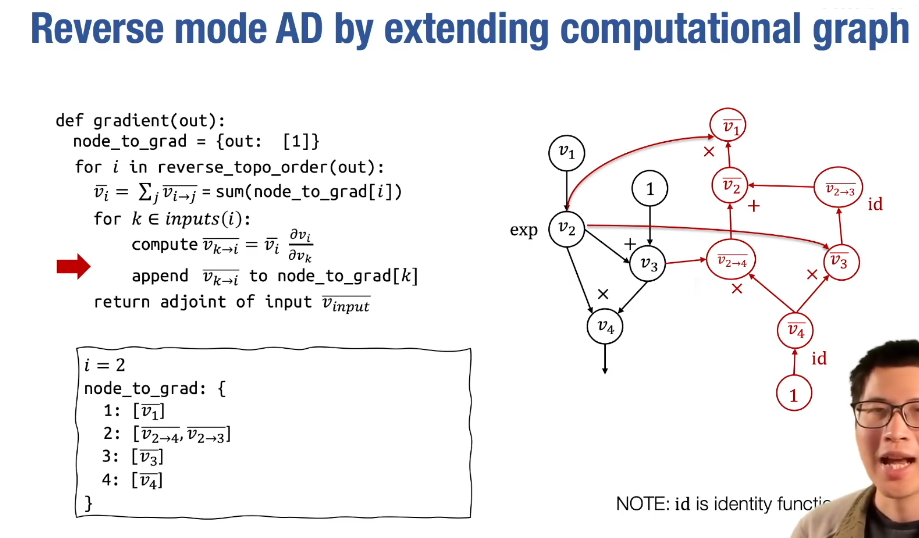
使用扩展计算图，可以方便计算梯度的梯度

• broadcast to 操作(从后往前比较维度，扩展缺失的或者为1的维度)求梯度，需要对扩展方向求和
• 求和操作求梯度，则使用broadcast to操作扩展为原shape
• 多维矩阵乘法只看最后两个维度，前面的维度扩展为相同的批次

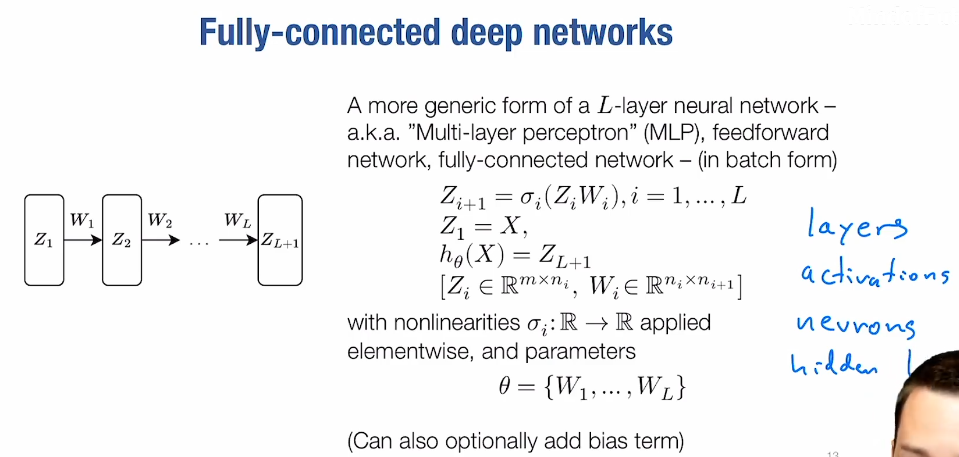
fully connected networks

• matrix broadcasting（does not copy any data）

• Newton’s Method

• momentum

  $$\begin{align*} u_t&=\beta u_{t-1} + (1-\beta) \Delta \\ \theta_t&=\theta_{t-1}-\alpha u_t \end{align*}$$

• unbiased momentum terms 让步长一致

  $$\begin{align*} u_t&=\beta u_{t-1} + (1-\beta) \nabla_\theta J(\theta_{t-1}) \\ \theta_t&=\theta_{t-1}-\alpha u_t/(1-\beta^{t}) \end{align*}$$

• nesterov momentum 在动量方向“未来位置”计算梯度，能提前感知参数更新后的地形，避免盲目跟随动量

  $$\begin{align*} v_t &= \gamma v_{t-1} + \eta \nabla_\theta J(\theta_{t-1} - \gamma v_{t-1}) \\ \theta_t &= \theta_{t-1} - v_t \end{align*}$$

• Adam

- weights initialization

neural network abstraction

• caffe 1.0 / tensorflow (静态计算图) / pytorch (动态计算图)

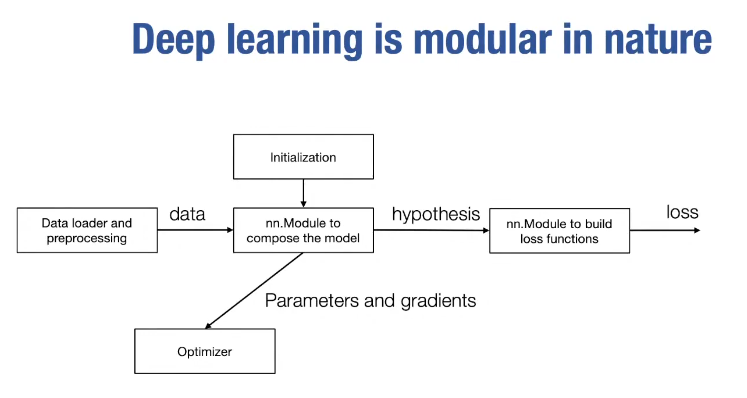
normalization and regularization

• 深度网络的权重初始化很重要，会导致不同的激活方差，但是可以通过normalization修正
• layer normalization / batch normalization

• batch normalization 导致依赖问题，训练时使用实际均值，测试时使用经验均值

• regularization 提高函数泛化性（模型参数数量大于样本数量
• l2 regularization / weight decay，添加正则化项，约束参数大小

• dropout 随机将激活值置为0

提供了类似于SGD的近似：

convolutional networks

• convolutions / padding / strided convolutions / pooling / grouped convolutions
• dilations

- 在自动微分中卷积梯度的中间结果较多，导致计算图较大，可以将卷积变为原子操作

• Z = batch * height * width * cin, W = k * k * cin * cout
• im2col

hardware acceleration

• vectorization 需要考虑内存对齐

• data layout and strides, strides 布局允许更灵活的数据变换（表示内存访问需要跳过的字节数

$$a[i * strides[0] + j * strides[1]]$$

• parallel for
• matrix multiplication

register tiled

cache line aware

both

why

gpu acceleration

• vector add

cpu side

• gpu memory

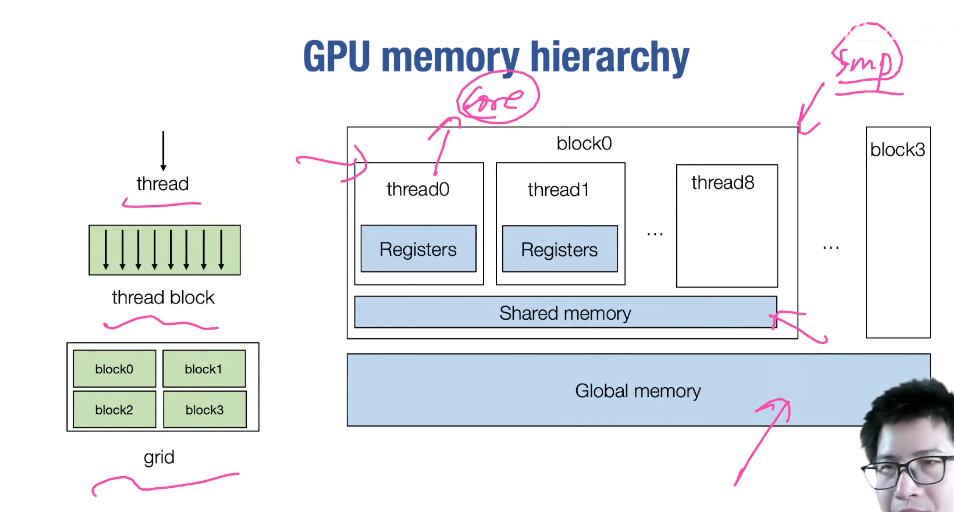
• window sum

• matrix multiplication

training large models

• reduce memory

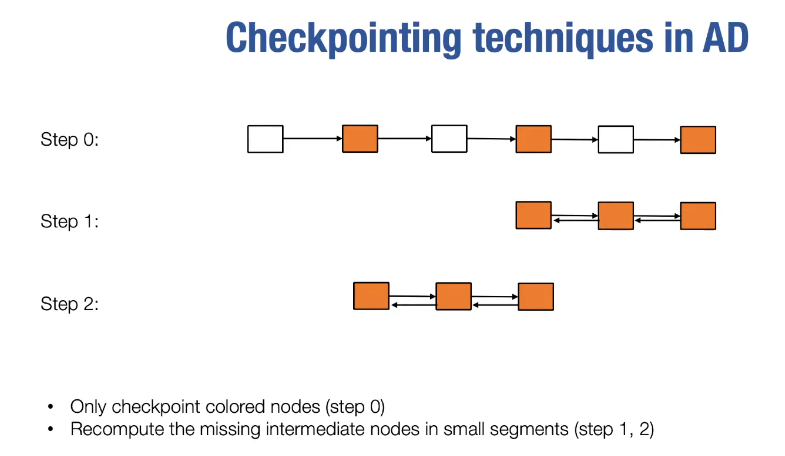
• all reduce
• parallel training(data parallel / model parallel)

generative adversarial networks

• 生成对抗网络：

• convolutional GAN
• cycle GAN

sequence modeling and recurrent networks

• recurrent neural networks

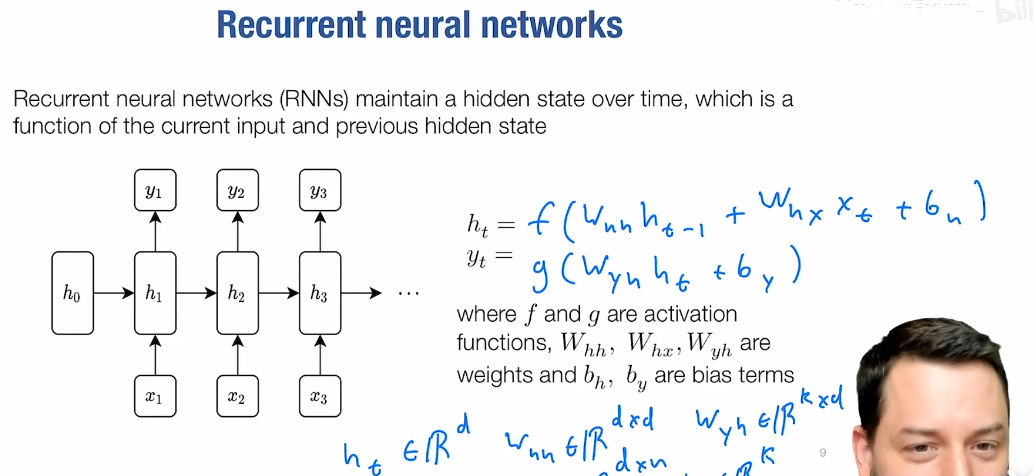
• stacking rnns
• lstm 解决梯度消失/爆炸问题

• seq2seq model / bidirectional rnns
• block training lstm

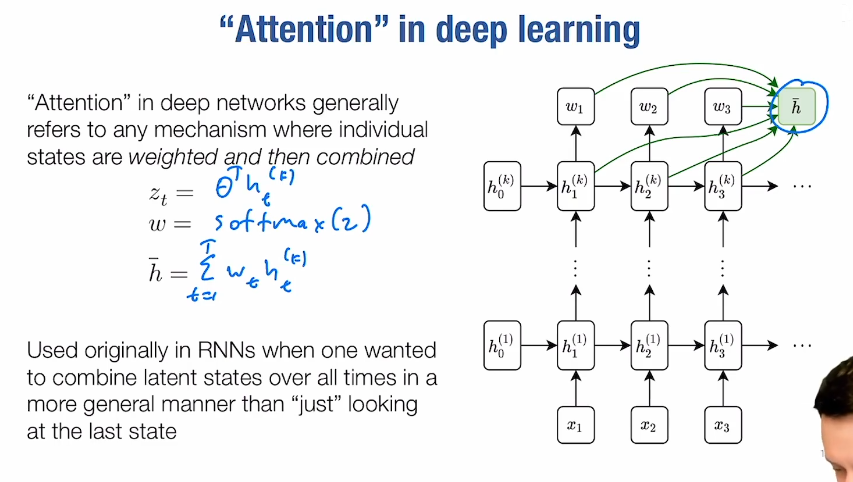
transformer

• attention

model deployment

• onnx
• machine learning complication